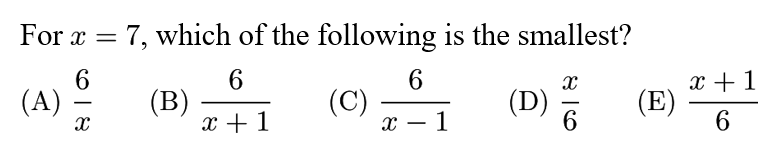
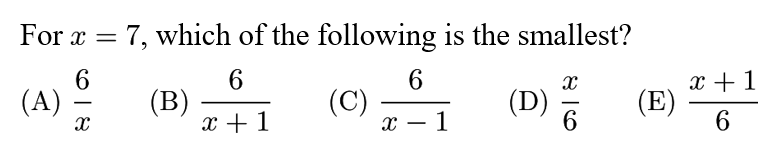
Answer: B
Solution:
A: 6/7 which is <1;
B: 6/8 < 6/7<1;
C: 6/6=1;
D: 7/6>1;E: 8/6>7/6>1.
The smallest is B.
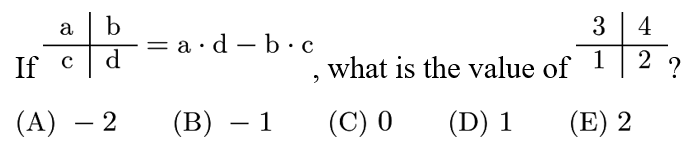
Answer: E
Solution:
=3*2-4*1=6-4=2.
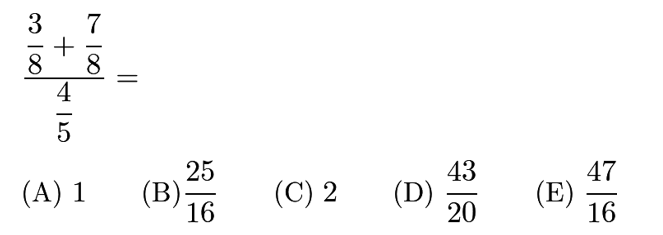
Answer: B
Solution:
=(10/8)/(4/5)=10/8*5/4=25/16.
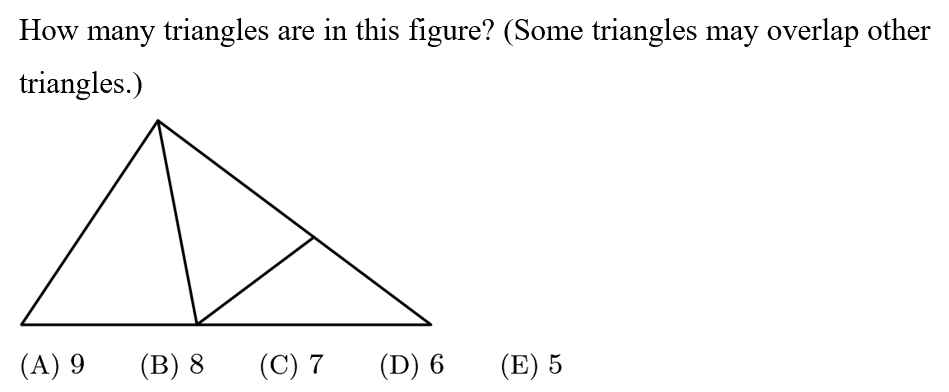
Answer: E
Solution:
By inspection, we have that there 5 triangles: Each of the 3 small triangles, 1 medium triangle made of the rightmost two small triangles, and the 1 large triangle.
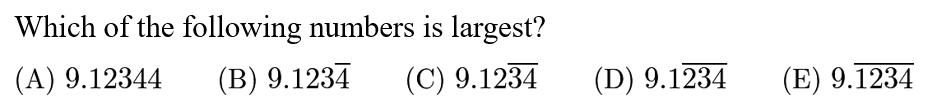
Answer: B
Solution:
A: 9.12344; B : 9.1234444; C: 9.12343434 ; D: 9.1234234; E: 9.12341234;

Answer: B
Solution:
By inspection, you can notice that the triangle on the top row matches the hole in the bottom row. This creates a 2*3 box, which has area 6.

Answer: D
Solution:
=(100*19.98)*(1.998*1000)=1998*1998=1998^2.

Answer: C
Solution:
30 days later: 200-30*0.5=200-15=185.
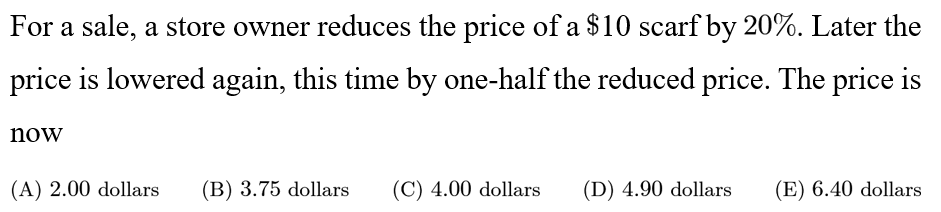
Answer: C
Solution:
=10*0.8*0.5=4

Answer: E
Solution:
3/1-4/2=3-2=1; so, W=3, Y+4; W+Y=7.

Answer: C
Solution:
Harry is a boy, there are 3 girls and 6 boys in his family. His sister, being a girl, would have 2 sister and 6 brother. Thus, S*B=2*6=12.
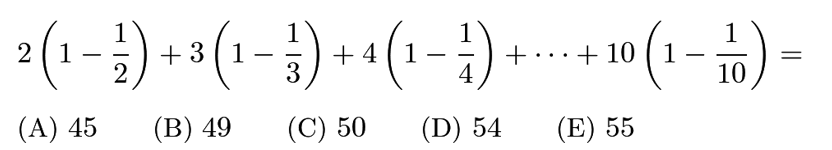
Answer: A
Solution:
=2*1/2+3*2/3+4*3/4+…+10*9/10=1+2+3+…+9=45.

Answer: C
Solution:
We can divide the large square into quarters by diagonals. Then, in 1/4 the area of the big square, the little square would have 1/2 the area. 1/4*1/2=1/8.

Answer: E
Solution:
If 80% of the people in the science club of 15 people are in the Math Club, 15*0.8=12 people are in the both the Math Club and the Science Club.
These 12 people are also 30% of the Math Club. There are 12/0.3=40 people in the Math Club.

Answer: D
Solution:
The population triples every 25 years from 200, and there are 50 years between 2000 and 2050, so we will have 200*3=600, 600*3=1800 . This is an underestimate, since there are actually 2 more years for the island's population to grow.
Therefore, 1800 can be rounded to 2000.

Answer: B
Solution:
We could triple the population every 25 years and make a chart:
Year: 2000-- Population: 200
Year: 2025-- Population: 600
Year: 2050-- Population: 1800
Year: 2075 --Population: 5400
Year: 2100-- Population: 16200
The closest year is 2075.

Answer: C
Solution:
We can divide the total area by how much will be occupied per person: 24900/1.5=16600 people can stay on the island at its maximum capacity.
In year 2100, the population is 16200, which is close to 16600. So it is 2100-2000=100 year s later.
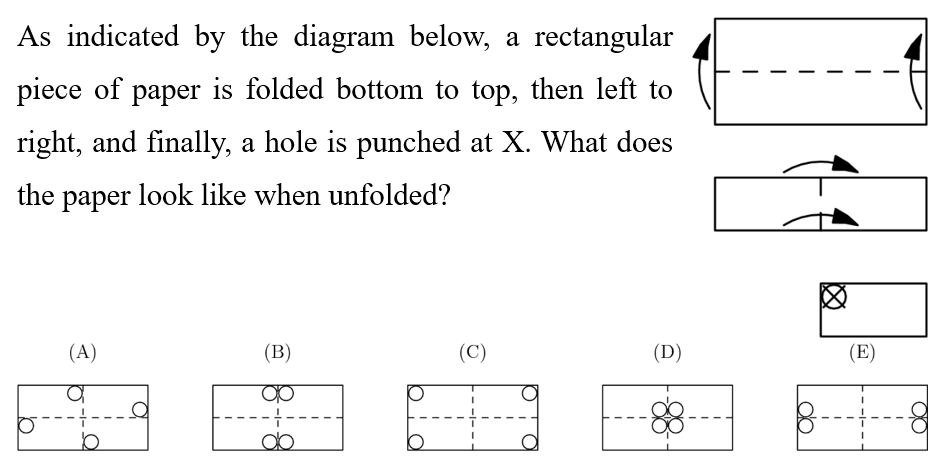
Answer: B
Solution:
By reversing the folds, we find that the holes will be
1) In the middle (in relation from left to right);
2) At separating poles (up and down);
This is pictured in B .

Answer: A
Solution:
The different possible (and equally likely) values Tamika gets are: 17(8+9); 18(8+10), and 19(9+10); The different possible (and equally likely) values Carlos gets are: 15(3*5), 18(3*6), and 30(5*6).
The probability that if Tamika had the sum 17 her sum would be greater than Carlos's set is 1/3, Because 17 is only greater than 15; The probability that if Tamika had the sum 18 her sum would be greater than Carlos's set is 1/3, because 18 is only greater than 15; The probability that if Tamika had the sum 19 her sum would be greater than Carlos's set is 2/3, because 19 is greater than both 15 and 18.
Each sum has a 1/3 possibility of being chosen, so we have
1/3*(1/3+1/3+2/3)=1/3*4/3=4/9.

Answer: D
Solution:
After both folds are completed, the square would become a triangle that has an area of 1/4 of the original square.
Since the area is 9 square inches for 1/4 of the square, 9*4=36 square inches is the area of square PQRS. The length of the side of a square that has an area of 36 square inches is 6 inches. Each side is 6 inches, so the total perimeter is 24 inches.
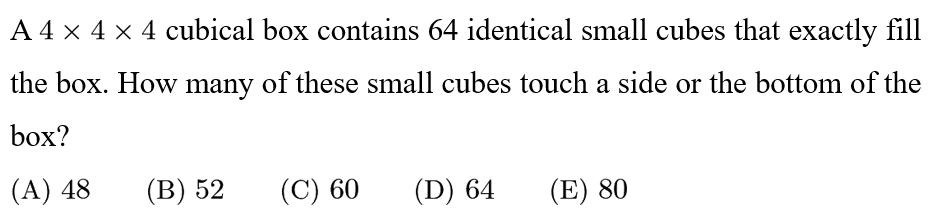
Answer: B
Solution:
You can imagine removing the cubes that do not fit the description of the problem, forming a "square cup". There are 4 cubes in the center of the top face that do not fit the description. Remove those. So does the second layer and the third layer. This means you removed 4+4+4=12 cubes of the 4*4*4=64 cubes. Thus, 64-12=52 cubes remain, and the answer is 52.

Answer: D
Solution:
We could start by looking for a pattern. 98, 49, 44, 22, 11, 6, 54, 27, 22, 11, 6,…
From here, we see that we have a pattern of 22, 11, 6, 54, 27, … after 98, 49, 44.
Our problem is find the 95th term of the sequence that goes 22,11,6,54,27,22,11,6,54,27,22,…… There are 5 terms in each repetition of the pattern, 95/5=0, so the answer is 27.
中文解析:
从98开始的一系列数,求第98项,一般都会有有数据重复的规律。 从第一项98, 按照规则2, 得到第二个数49; 根据规则3, 得到第三个数44; 根据规则2, 得到第四个数22; 根据规则2, 得到第五个数11; 根据规则3, 得到第六个数6; 根据规则1, 得到第七个数54; 根据规则2, 得到第八个数27; 根据规则3,得到第九个数22, 这与第四个数重复,即从第四项22开始,出现重复数项: 22, 11,6, 54, 27, 22, 11,6, 54, 27, 22,...... 第98项: (98-3) /5, 余数是0;因此第98项是27. 答案是D。
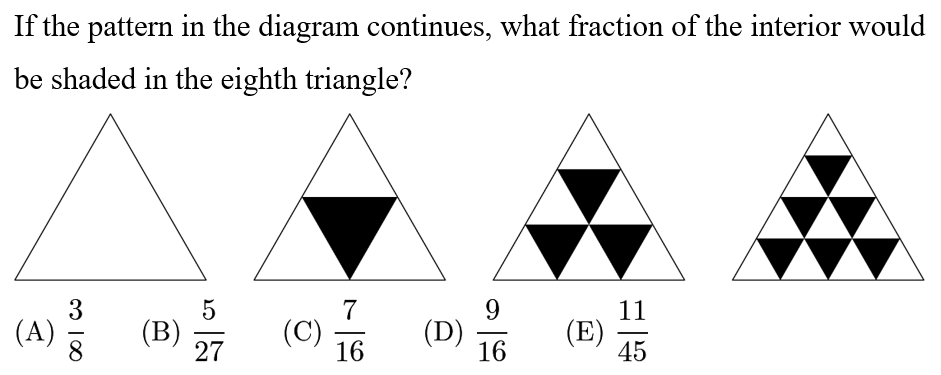
Answer: C
Solution:
All small triangles are congruent in each iteration of the diagram. The number of shaded triangles follows the pattern: 0, 1, 3, 6…. Each time, the number 1,2,3,4,5… is added to the previous term. Thus, the first eight terms are: 0, 1, 3, 6, 10, 15, 21, 28.
In the eighth diagram, there will be 28 shaded triangles. The total number of small triangles follows the pattern: 1, 4, 9, 16. …which is the pattern of "square numbers". Thus, the eighth triangle will be divided into 8^2=64 small triangles in total.
The ratio of shaded to total triangles will be the fraction of the whole figure that's shaded, since all triangles are congruent. Thus, the answer is 28/64=7/16.
中文解析:
第二个图形: 不论黑色白色,总共有4个小三角形, 其中黑色的有1个,因此黑色部分占比是1/4.
第三个图形: 不论黑色白色,总共有9个小三角形,其中黑色的有3个,因此黑色部分占比是3/9.
第四个图形: 不论黑色白色,总共有16个小三角形,其中黑色的有6个,因此黑色部分占比是6/16.
从第二个图形起的规律: 不论黑色白色,总共小三角形的个数的规律是: 4, 9, 16, 25, 36, 49, 64......
其中黑色小三角形个数的规律: 1, 3, 6, 10, 15, 21, 28......
因此第八个图形, 小三角形的总数是64个,其中黑色的是28个,黑色占比是28/64, 约分后即: 7/16,答案是C。

Answer: E
Solution:
The numbers that are shaded are 1, 3, 6, 10, 15, 21, 28,…which adding 1, 2,3,4,5,6,…
When you divide each of those numbers by 8, all remainders must be present.
Quickly scanning the list, that smaller list doesn't have any multiples of 8 until it hits 120. So 120 must be the answer.
中文解析:
按照提意涂黑色的小方块分别是: 1, 3, 6, 10, 15, 21, 28, 36,45, 55 ...... ( Triangular Number Sequence
)其中每项都在前一项的基础上分别增加2, 3, 4,5,6,7,8,9,....... 或者第n项是:n(n+1)/2。 当每一列都有被涂黑色时满足题目要求。 也就是说这个序列的数字除以8的余数要覆盖了0,1,2,3,4,5,6,7时满足题目要求。 我们记录下这序列数除以8的余数分别是: 1, 3, 6, 2, 7, 3, 4,4,5,7,2,6,3,1,0. 最后一个余数0 对应的是120. 答案是E。
Answer: D
Solution:
If Toy had 36 dollars at the beginning, then after Amy doubles his money, he has 36*2=72 dollars after the first step. Then Jan doubles his money, and Toy has 72*2=144 dollars after the second step. Then Toy doubles whatever Amy and Jan have. Since Toy ended up with 36, he spent 144-36=108 to double their money. Therefore, just before this third step, Amy and Jan must have had 108 dollars in total. And, just before this step, Toy had 144 dollars. Altogether, the three had 144+108=252 dollars, and the correct answer is D.
中文解析:
Toy最初由有36元, Amy给他36元后, Toy变成72元。 Jan给Toy72元, Toy变成144元。 接下来, Toy要给Amy和Jan钱,给出之后,Toy变成了36元,说明Toy 给Amy和Jan的钱是144-36=108元。 Toy给Amy和Jan的钱需要double Amy和Jane本来的钱数。 这说明Amy和Jan合起来有108元,接受了Toy给的钱后,变成了108+108=216元。 因此最后的状态,三个人的钱数和是: 36+216=252元。 答案是D。
AMC培训、答疑,请联系微信 / 电话:136 1118 1627
艾蕾特教育 @Elite Edu, 在这里,